新闻资讯

微孔为孔宽小于2 nm的孔，通过气体吸附的方法测试样品的等温线，然后进行孔径分析测试，微孔分析模型有Horvath-Kawazoe(HK)和 Saito-Foley(SF)法、DR、DA(DR理论的扩展)、T-Plot方法等，本次内容将介绍HK/SF微孔分析方法。

HK方法将吸附质液体（液氮）限制在狭缝孔内（这些孔常见于某些碳分子筛和活性炭内）。

此方法的理论假定为：

1）充满给定大小的微孔，需要一定的压力。如果吸附压力小于该压力则微孔是完全空的；反之，则被完全填满；

2）吸附热在热力学上的行为为二维理想气体，经过热力学讨论，考虑了吸附剂-吸附质之间的作用和吸附质-吸附质-吸附剂相互作用，得到表达式：

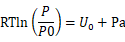
由于微孔环境不适合开尔文方程，所以引入势函数，吸附势能的计算是借用描述两个石墨碳原子层平面间的作用势能来代替，遵循 E-P 模型，且考虑到孔内吸附质分子的作用加强了孔间作用势能，得到势能函数：

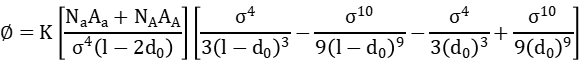
认为吸附过程是二维凝聚吸附过程，即吸附势能等于凝聚过程所做的功，即得到：

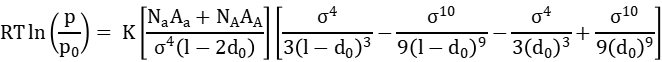
式中，l 应大于 d0，K 是阿伏伽德罗常数，d0是吸附剂原子和吸附质分子直径的算术平均值，Na和 NA分别为单位比表面积的原子和分子数。而 Aa和 AA是;

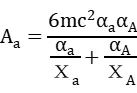
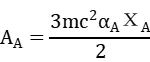
式中，m 是电子的质量，c 是光速，αa、 Хa和αA 、ХA分别是吸附剂原子和吸附质分子的极化率和磁化率。

σ可由下式计算：

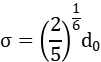
HK 计算模型可以得到微孔分布、微孔孔容积、最可几孔径结果。

S-F模型：

Saito和Foley将HK法扩展到87K时氩气在沸石分子筛上的吸附等温线计算有效孔径分布，S-F法同样基于E-P势能方程不同的时假设孔是圆柱形孔，依据HK对数运算式，SF导出了一个类似于HK方程的关系式：

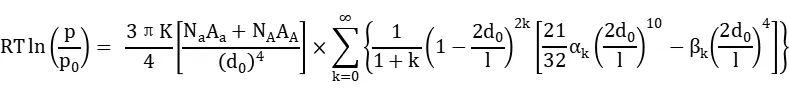
式中，k是加和的正整数，α_k 和β_k 按下式求得：

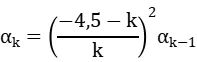
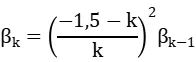
其余符号的意义与H-K方程中的相同。

优点：HK 在计算狭缝类活性炭样品方面，能得到令人满意的分布结果，同时采用不同的分子探针，能得到很好的一致性。

局限性：公式中涉及到吸附质与吸附剂的极化率和磁化率，所以采用不同的吸附剂，或者在不同的吸附质上吸附，需要知道其对应的物理常数。而且不同的孔结构模型需要不同的计算公式，计算比较麻烦。

国仪精测的V-SORB X800系列比表面积及孔径分析仪全程通过软件全自动操作，只需要对软件进行参数选择即可，分析过程如下图所示：

1）首先要确认材料的孔的特性，包括层片状孔、狭缝型的孔、圆柱型的孔等；

2）确定孔的特性后，选择分析模型，包括扁平孔HK模型和柱形孔SF，一般活性炭等层片状材料对应的是HK模型，分子筛等圆柱型形的孔对应的是SF模型；

3）然后选择吸附剂类型：根据不同材料选择不同的吸附剂类型，包括：Aluminosilicate（铝硅酸盐）、Aluminophosphate（磷酸铝）、Carbon-Graphite(Ross/Olivier)、Carbon-Graphite(HK)、Zeolite（沸石）、软件操作见下图所示，图内任意部位点右键，弹出对话框进行模型选择、吸附剂吸附质选择、孔径选择、和删除选择点，图显示得结果会有所不同。

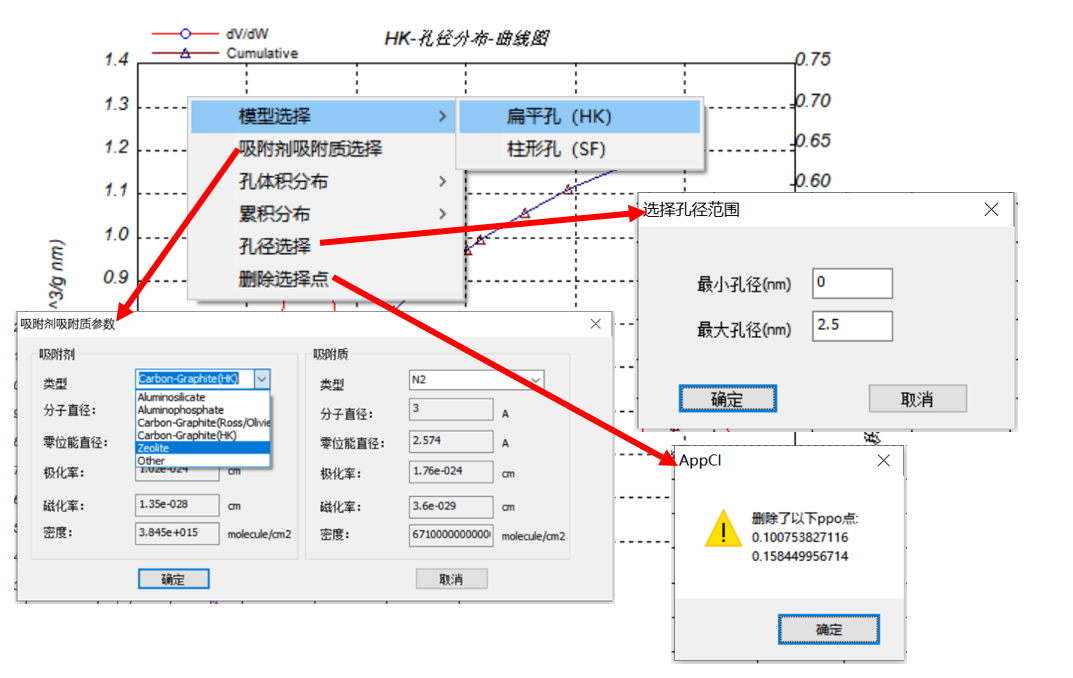
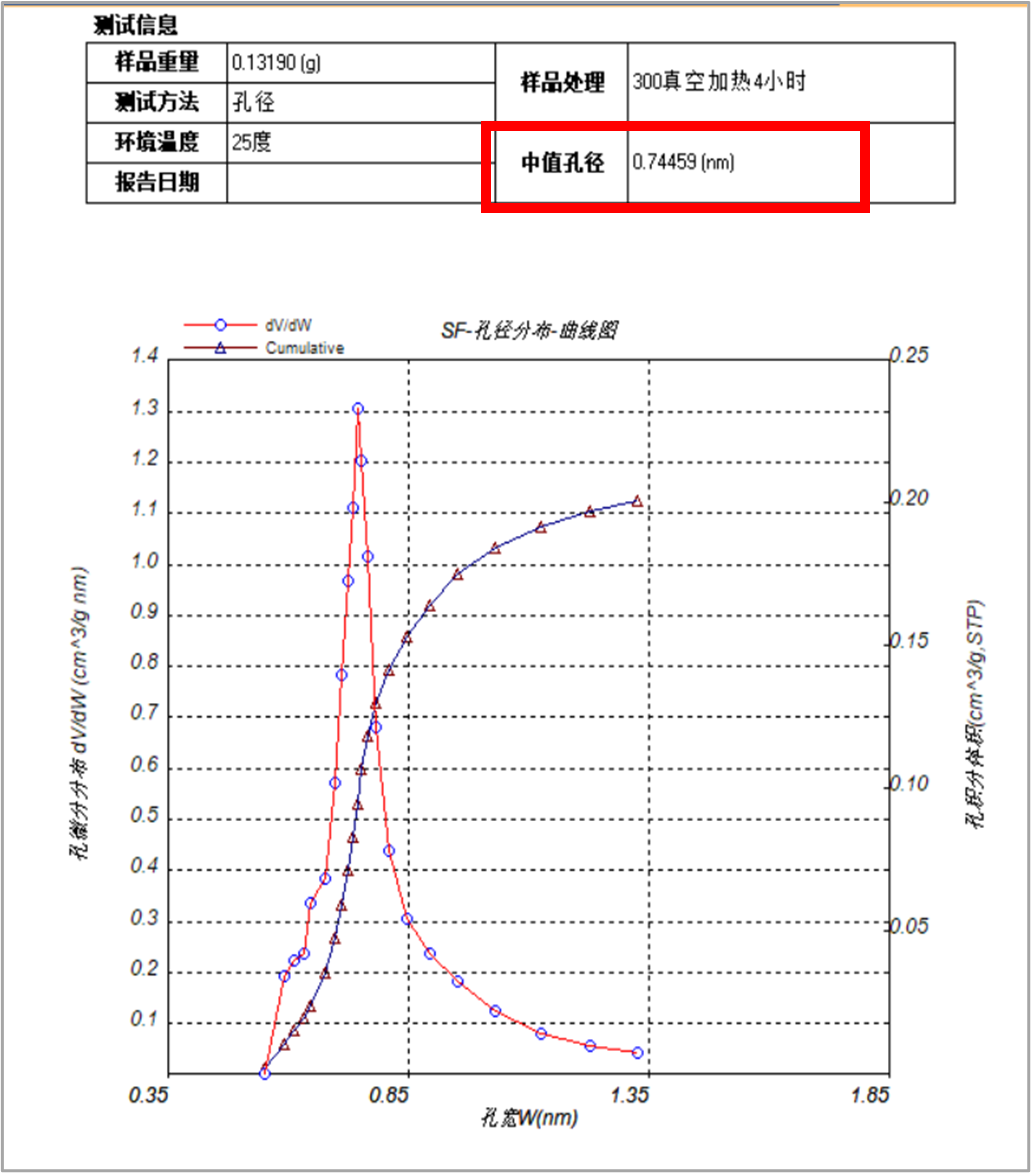
通过以上分析最后可得出微孔分析结果见下图，微孔孔径分布和中值孔径（最可几孔径），从而分析出样品中微孔信息。

气体吸附技术在氢能及氢燃料电池行业中的应用.pdf

扫码获取完整报告